Since the mid-1940s, compounds containing the mineral fluoride have been added to community water supplies throughout the U.S. to prevent tooth decay. Health concerns expressed … Continue reading “Is Fluoridated Water Safe?”
Barrie Damson, AB ’56, is a dedicated Harvard Chan champion. He feels so close to the School that he refers to the students as … Continue reading “Damson Family Gift Funds Financial Aid”
Message from the Acting Dean: The Ripple Effect The School’s alumni have created waves of change wherever they bring their skills and ideals. Winter … Continue reading “Winter 2016”
[Winter 2016] The stories in this issue of Harvard Public Health demonstrate the extraordinary ripple effect that our School’s graduates are having on populations … Continue reading “Message From the Acting Dean: The Ripple Effect”
[Winter 2016] Parents Chemical Exposures May Affect Their Children Parents’ exposure to chemicals found in common household items such as paints and plastic bottles … Continue reading “Winter 2016 Frontlines”
[Winter 2016] Leadership Council Annual Meeting From Cells to Cell Phones The annual summit of the School’s Leadership Council on October 29 and 30 … Continue reading “Events 2015”
[Winter 2016] Dear friends, This issue of Harvard Public Health celebrates our alumni and highlights the extraordinary “ripple effect” we see in public health, … Continue reading “Letter from the Vice Dean: A Season of Gratitude”
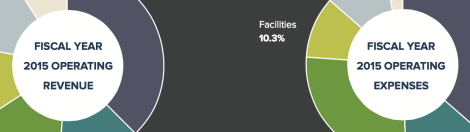
[Winter 2016] The Harvard T.H. Chan School of Public Health continues to pursue its strategy of revenue diversification and expense management on the path … Continue reading “Fiscal Year 2015 Financial Highlights”
[Winter 2016] Jeremiah Zhe Liu, SM ’15, PhD ’20, is creating new biostatistical methods that may help reverse the devastating effects of air pollution … Continue reading “Blue Sky Scenario”
[Winter 2016] As executive director of The Innocence Project, Madeline deLone works to free wrongfully convicted people from prison using DNA evidence. Since 2004, … Continue reading “A Matter of Conviction”