Analytic Methods

Our primary analytic approach for describing socioeconomic gradients by area-based socioeconomic measures has been to use geocodes to append area-based socioeconomic data to case records, to stratify these records into discrete categories based on ABSM, and to aggregate numerators and denominators over areas, within levels defined by ABSM. This method avoids the problem of unstable rates arising from small areas by assuming that cases and population denominators from areas with similar socioeconomic characteristics can be legitimately combined into the same strata. An alternative approach, which preserves the spatial information of the geocodes, is discussed in the section on multilevel analyses.

The following steps are used to generate age-standardized disease rates stratified by area-based socioeconomic measures, once the case data have been geocoded and appropriate ABSMs have been generated from census data.

• Aggregate the case data into numerators (age cells within areas/geocodes).
• Aggregate population denominator data into age cells within areas/geocodes.
• Merge the numerators and denominators with ABSMs, by area/geocode.
• Aggregate over areas into strata defined by categorical ABSM and age category.
• Generate age-standardized rates and other summary measures.

[See the ‘Tools” section for a step by step comparison of the analytic methods, the relevant task of the Case Example, and sample SAS code.]

Aggregating Numerator Data

Data from public health databases are typically formatted such that each record represents one person (or case report). Once these data have been geocoded, they need to be aggregated before linking to denominator and ABSM data. Before aggregating, however, one should exclude all records that are not geocoded, do not meet the case definition, or are missing data on the important covariates (e.g. age, in the case of simple age-standardized analyses; age, sex, and race/ethnicity in the case of more complex stratified analyses).

One can think of the basic unit of aggregation as a cell, defined by age and other covariates, within an area/geocode. Once aggregated, this cell within an area can be linked to a relevant population denominator. The cell contains a count of all cases within that area that meet the specified age and other covariate criteria. Since our goal is eventually to create rates, we call this count of cases the “numerator.”

Example:
We intend to age-standardize in 5 broad age categories, 0-14, 15-24, 25-44, 45-64, 65+. Therefore, we need to aggregate the records in each census tract into cells defined by the corresponding ages. As an example, consider the following 23 records from census tracts 25009250500 and 25009250800.

Before aggregating:
Record #	Geocode	Age of death
1	25009250500	<1
2	25009250500	<1
3	25009250500	<1
4	25009250500	17
5	25009250500	19
6	25009250500	27
7	25009250500	38
8	25009250500	40
9	25009250500	40
10	25009250500	44
11	25009250800	<1
12	25009250800	<1
13	25009250800	5
14	25009250800	22
15	25009250800	24
16	25009250800	26
17	25009250800	31
18	25009250800	36
19	25009250800	36
20	25009250800	40
21	25009250800	43
22	25009250800	43
23	25009250800	43
After aggregating:
Geocode	Age category	Number of deaths (numerator)
25009250500	0-14	3
25009250500	15-24	2
25009250500	25-44	5
25009250800	0-14	3
25009250800	15-24	2
25009250800	25-44	8

Aggregating Denominator Data

Denominator data at the census tract level typically come from the decennial census. In 1990, the US Census reported population counts by age in 31 categories (<1, 1-2, 3-4, 5, 6, 7-9, 10-11, 12-13, 14, 15, 16, 17, 18, 19, 20, 21, 22-24, 25-29, 30-34, 35-39, 40-44, 45-49, 50-54, 55-59, 60-61, 62-64, 65-69, 70-74, 75-79, 80-84, 85+). In the 1990 US Census STF3, age specific population counts were reported in table P013. Variable P0130001 gave the count of residents <1 year old, P0130002 gave the count of residents 1-2 years old, etc.

For the purposes of age standardization, these age categories need to be re-aggregated to match the age categories used for categorizing case data (numerators, above) and the age categories from the standard million reference population. Additionally, when using case data from multiple years, in order to calculate an average annual incidence rate, one needs to use a person-time denominator (population count multiplied by number of years of case data). For example, in the case of the Massachusetts all-cause mortality data, we have three years worth of cases (1989-1991). Therefore, we multiply the population count in each age category by 3.

Example:
For census tract 25009250800 in 1990, we wish to age standardize using the same five broad age categories as in the numerator example above (0-14, 15-24, 25-44, 45-64, 65+):

Before:
Census variable	Ages (years)	Population count
P0130001	<1	115
P0130002	1-2	243
P0130003	3-4	197
P0130004	5	92
P0130005	6	59
P0130006	7-9	237
P0130007	10-11	160
P0130008	12-13	141
P0130009	14	77
P0130010	15	62
P0130011	16	54
P0130012	17	94
P0130013	18	65
P0130014	19	89
P0130015	20	101
P0130016	21	128
P0130017	22-24	387
P0130018	25-29	571
P0130019	30-34	746
P0130020	35-39	422
P0130021	40-44	354
P0130022	45-49	317
P0130023	50-54	176
P0130024	55-59	174
P0130025	60-61	65
P0130026	62-64	214
P0130027	65-69	158
P0130028	70-74	316
P0130029	75-79	178
P0130030	80-84	112
P0130031	85+	69

In order to collapse these variables into the five broad age categories, we have to sum up census variables as follows:

After:
Age category	Population count		Person-time denominator (x 3 years of case data)
P0130001	<1	1321	115
P0130002	1-2	980	243
P0130003	3-4	2093	197
P0130004	5	946	92
P0130005	6	833	59

Merging numerators with denominators and ABSM

Once the numerators and denominators have the same structure (AREAKEY x AGECAT), they can be merged together, along with the ABSM data (by AREAKEY). For age cells within areas where no cases were reported, we set the numerator to zero.

Example:

Before merging with ABSM:
Numerator dataset:
Geocode/Areakey	Age category	Number of deaths (numerator)
25009250500	0-14	3
25009250500	15-24	2
25009250500	25-44	5
25009250500	45-64	7
25009250500	65+	26
25009250800	0-14	4
25009250800	15-24	3
25009250800	25-44	8
25009250800	45-64	13
25009250800	65+	132
Denominator dataset:
Geocode/Areakey	Age category	Person-time denominator (x 3 years of case data)
25009250500	0-14	4152
25009250500	15-24	1953
25009250500	25-44	3489
25009250500	45-64	1233
25009250500	65+	1212
25009250800	0-14	3963
25009250800	15-24	2940
25009250800	25-44	6279
25009250800	45-64	2838
25009250800	65+	2499

After merging with ABSM:
Geocode	Age category	Poverty	Numerator	Denominator
25009250500	1	4	3	4152
25009250500	2	4	2	1953
25009250500	3	4	5	3489
25009250500	4	4	7	1233
25009250500	5	4	26	1212
25009250800	1	3	4	3963
25009250800	2	3	3	2940
25009250800	3	3	8	6279
25009250800	4	3	13	2838
25009250800	5	3	132	2499

Aggregating OVER areas in ABSM strata

Next, in order to generate rates for categories of a specific ABSM, it is necessary to aggregate OVER areas into strata defined by AGECAT and ABSM. Numerators and denominators from census tracts with missing ABSM data for a particular ABSM are typically excluded from that analysis.

Example: In Suffolk County, Massachusetts, there are a total of 189 census tracts. We wish to examine all cause mortality rates by poverty, with poverty categorized into 4 strata (0-4.9%, 5-9.9%, 10-19.9%, and 20-100%).

ABSM: CT Poverty	Number of census tracts
0.0-4.9%	10
5.0-9.9%	37
10.0-19.9%	56
20.0-100.0%	83
Missing poverty data	3

Thus, to obtain the mortality rates in the least impoverished stratum (0.0-4.9% below poverty), we need to aggregate the cases and the population at risk OVER the ten census tracts in that stratum (preserving the age structure WITHIN each poverty stratum so that we can age standardize in the following step, below). For the next poverty stratum (5.0-9.9%) we need to aggregate the cases and the population denominator over 37 census tracts, and so on. Cases and population at risk in the three census tracts with missing poverty data are excluded from the analysis.

This yields the following table:

ABSM: CT poverty	Age category	Numerator	Denominator
0.0-4.9%	0-14	1	10,608
0.0-4.9%	15-24	5	9,984
0.0-4.9%	25-44	54	29,190
0.0-4.9%	45-64	106	16,710
0.0-4.9%	65+	657	15,825
5.0-9.9%	0-14	40	69,939
5.0-9.9%	15-24	39	64,065
5.0-9.9%	25-44	252	179,595
5.0-9.9%	45-64	792	90,042
5.0-9.9%	65+	4,535	80,916
10.0-19.9%	0-14	101	88,989
10.0-19.9%	15-24	93	93,147
10.0-19.9%	25-44	531	224,793
10.0-19.9%	45-64	962	100,479
10.0-19.9%	65+	3,944	71,955
20.0-100.0%	0-14	182	155,193
20.0-100.0%	15-24	170	217,593
20.0-100.0%	25-44	831	288,882
20.0-100.0%	45-64	1,291	108,588
20.0-100.0%	65+	3,645	72,720

Generating Rates and Other Summary Measures/Measures of Effect

1. Age-standardized incidence rates

The standard practice of public health departments in reporting population rates of mortality and disease incidence is to calculate age-standardized rates, which facilitates comparisons between regions or subgroups of interest. The age-standardized rate is interpretable as the rate that would be observed in a population if that population had the same age distribution as a given reference population. Standardization by the direct method involves taking a weighted average of the age specific incidence rates observed in the area or subgroup of interest, where the weights come from a standard age distribution, such as the year 2000 standard million $(1)$ .

“Standard million” reference populations are available based on the US population age distribution for 1940, 1970, 1980, 1990, and 2000. Here we present the standard million in 11 age categories.

Age (years)	Standard million reference population
Age (years)	Year 1940	Year 1970	Year 1980	Year 1990	Year 2000
<1	15,343	17,150	15,598	12,936	13,818
1-4	64,718	67,265	56,565	60,863	55,317
5-14	170,355	200,511	154,238	141,584	145,565
15-24	181,677	174,405	187,542	147,860	138,646
25-34	162,066	122,567	163,683	173,600	135,573
35-44	139,237	113,616	113,155	151,095	162,613
45-54	117,811	114,265	100,641	101,416	134,834
55-64	80,294	91,481	95,799	85,030	87,247
65-74	48,426	61,192	68,775	72,802	66,037
75-84	17,303	30,112	34,116	40,429	44,842
85+	2,770	7,436	9,888	12,385	15,508

For our project, we used five broad age categories to age standardize, in order to obtain more stable rates in each age stratum, particularly for outcomes with sparse data. The relationship between our five categories and the standard eleven categories is illustrated in the table below.

Age in 11 categories	Year 2000 standard million	Age in 5 categories	Year 2000 standard million
<1	13,818	<15	214,700
1-4	55,317
5-14	145,565
15-24	138,646	15-24	138,646
25-34	135,573	25-44	298,186
35-44	162,613	25-44	298,186
45-54	134,834	45-64	222,081
55-64	87,247	45-64	222,081
65-74	66,037	65+	126,387
75-84	44,842
85+	15,508

If $cases_j$ represents the number of cases in age group j of the group or region of interest and $pop_j$ represents the population associated with that age group, then the standardized rate $IR_{st}$ for the group or region is

$\displaystyle IR_{st} =\frac{\sum_j w_j \left(\frac{\mbox{cases}_j}{\mbox{pop}_j}\right)}{\sum_j w_j} = \frac{\sum_j w_j IR_j}{\sum_j w_j}$

where $w_j$ is the weight associated with category j in the reference (standardizing) population (e.g. the population size or the proportion of the total population). The estimated variance of the standardized rate is given by:

$\displaystyle Var(IR_{st})=\frac {{\sum_j {w^2}_j} {\left(\frac{\mbox{cases}_j}{\mbox{pop}^2_j}\right)}} {\left({\sum_j w_j}\right)^2}$

(When the $w_j$ s are proportions, then $\displaystyle IR_{st} ={\sum_j w_j IR_j}$ and $\displaystyle Var(IR_{st})={\sum_j {w^2}_j} \left(\frac{\mbox{cases}_j}{\mbox{pop}^2_j}\right)$ ).

Example:
To calculate the age-standardized all cause mortality rates in each of the four poverty strata in Suffolk County, we start with the age-specific mortality data. In each poverty stratum, the age standardized mortality rate is calculated as a weighted sum of the age-specific mortality rates, with the weights for each age stratum defined by the Year 2000 standard million.

ABSM: CT poverty	Age category	Numerator	Denominator	Year 2000 standard million	$w_ j$ (weight)	$IR_j$ (incidence rate per 100,000)	$IR_{st}$ (age standardized rate per 100,000)
0.0-4.9%	0-14	1	10,608	214,700	0.215	9.4	729.7
0.0-4.9%	15-24	5	9,984	138,646	0.139	50.1
0.0-4.9%	25-44	54	29,190	298,186	0.298	185
0.0-4.9%	45-64	106	16,710	222,081	0.222	634.4
0.0-4.9%	65+	657	15,825	126,387	0.126	4,151.70
5.0-9.9%	0-14	40	69,939	214,700	0.215	57.2	966.2
5.0-9.9%	15-24	39	64,065	138,646	0.139	60.9
5.0-9.9%	25-44	252	179,595	298,186	0.298	140.3
5.0-9.9%	45-64	792	90,042	222,081	0.222	879.6
5.0-9.9%	65+	4,535	80,916	126,387	0.126	5,604.60
10.0-19.9%	0-14	101	88,989	214,700	0.215	113.5	1,014.0
10.0-19.9%	15-24	93	93,147	138,646	0.139	99.8
10.0-19.9%	25-44	531	224,793	298,186	0.298	236.2
10.0-19.9%	45-64	962	100,479	222,081	0.222	957.4
10.0-19.9%	65+	3,944	71,955	126,387	0.126	5,481.20
20.0-100.0%	0-14	182	155,193	214,700	0.215	117.3	1,019.30
20.0-100.0%	15-24	170	217,593	138,646	0.139	78.1
20.0-100.0%	25-44	831	288,882	298,186	0.298	287.7
20.0-100.0%	45-64	1,291	108,588	222,081	0.222	1,188.90
20.0-100.0%	65+	3,645	72,720	126,387	0.126	5,012.40

2. Confidence intervals for directly standardized rates

Traditional confidence limits for the direct standardized rates are based on the normal distribution and require large cell counts. In our analyses, we found that they can also occasionally result in “impossible” lower limits that are less than zero. Because of this, we adopted an alternate method for calculating the confidence limits based on the inverse gamma function $(2)$ . This method assumes that the direct standardized rate is a linear combination of independent Poisson random variables. Assuming that this linear combination also follows a Poisson distribution, the age-standardized rate E(X) = x follows a gamma distribution Γ(a,b) as follows:

$\displaystyle X \backsim \Gamma \left(\frac{x^2}{v}{,} \frac{v}{x} \right)$

where x is the age-standardized rate ( $IR_{st}$ as estimated above) and v is its variance, as described above. Converting this to the gamma distribution in its standard form, i.e. where b=1, this yields

$\displaystyle \frac{X}{b} \backsim \Gamma \left(\frac{x^2}{v}{,}1 \right)$

which greatly simplifies calculations. Then the lower 100(1-α) confidence limit for $\displaystyle \frac{x^2}{v}$ is given by

L $\displaystyle \left( \frac{x^2}{v} \right)= \Gamma^{-1} \left( \frac{x^2}{v}{,}1 \right) \left( \alpha \diagup {2} \right)$

and the upper 100(1-α) confidence limit for $\displaystyle \frac{x^2}{v}$ is given by

U $\displaystyle \left( \frac{x^2}{v} \right) = \Gamma^{-1} \left(\frac {(x+{k_M})^2}{(v+k_M)}{,}1 \right) \left(1-\frac {\alpha} {2}\right)$

where $k=k_M=\mbox{max}_{je\left(1,...,j\right)} \left(k_j\right)$ is a continuity correction necessitated by using a continuous distribution to estimate confidence limits for a discrete random variable.

Increasing the number of events by 1 in an age stratum i results in a $\displaystyle k_j=\frac{w_j}{pop_j}$ increase in the age-standardized rate. If $k_j$ is constant for all age intervals, then $k_j = k$ . However, since the $w_j$ and $pop_j$ typically vary across age strata, it is unclear what value of k to use. A very conservative upper limit can be obtained by using the maximum value of $k_j = k_M$ . However, following the recommendation of the NCHS, we used a close approximation that alleviates the need to calculate $k_M$ :

U $\displaystyle \left( \frac{x^2}{v} \right) = \Gamma^{-1} \left(\frac{x^2}{v}+{1,1}\right)\left(1-\frac {\alpha} {2}\right)$

To transform these intervals to obtain the desired confidence limits for X, we use L(X) = $\displaystyle \frac {L\left(x^2 \diagup v \right)}{x \diagup v}$ and U(X) = $\displaystyle \frac {U\left(x^2 \diagup v \right)}{x \diagup v}$ .

Example:
In the following analysis of mortality due to homicide and legal intervention among hispanic women in Massachusetts, the lower confidence limits on the rate in the 5.0-9.9% poverty stratum is negative, using the traditional normal approximation method. In contrast, the lower confidence limit based on the gamma distribution yields a more reasonable confidence limit.

ABSM: CT poverty	Rate per 100,000	Confidence Limits				Deaths	Person-time at risk
		Normal approximation		“Gamma” interval
		Lower	Upper	Lower	Upper
0.0-4.9%	0	(0.0	,0.0)	(0.0	,9.2)	0	40,182
5.0-9.9%	3.5	-(0.5	,7.5)	(0.7	,10.3)	3	67,458
10.0-19.9%	3.8	(0.1	,7.5)	(1.0	,9.7)	4	87,336
20.0-100.0%	4.2	(1.4	,7.0)	(1.9	,8.0)	11	228,288

3. Confidence intervals for IRst

When the observed rate is zero (i.e. there were zero cases), the gamma method is unable to produce confidence limits for the direct standardized rates. In this situation, we adopt the following convention for the confidence limit. The lower limit is simply set to zero. For the upper limit, we assume that the number of cases (i.e. the count) follows a Poisson distribution, and use the formula for the “exact” upper confidence limit of a Poisson random variable $(3)$ :

U(Y) = $\displaystyle \frac{1}{2}\chi^{-1}_{2\left(y+1\right)df} \left(1-\frac{\alpha}{2} \right)$

where y is the count, i.e. zero. When α = 0.05 (i.e. for a 95% confidence limit) this simplifies to U(Y) = $\displaystyle \frac{\chi^{-1}_{2df}\left({1-\alpha \diagup 2}\right)}{2}$ = 3.689.

We can then divide this upper limit on the count by the population denominator to give the upper limit on the rate.

Example:
In the analysis of mortality due to homicide and legal intervention among Hispanic women in Massachusetts, the estimated rate in the least impoverished group is zero, since there were no deaths reported in census tracts with 0-4.9% below poverty. In the table below, the normal approximation method yields a confidence interval of (0,0) for the rate in the least impoverished group, as well (as “impossible” negative lower limits on the rates in the 5.0-9.9% poverty stratum, as we saw above). The gamma method also yields a (0,0) interval for the rate in the least impoverished group, so we have corrected the entry for the upper confidence limit as described above. Using the “exact” upper limit on the count of 3.689, we divide this by the denominator (40,182) to give an upper limit of 9.2 per 100,000.

ABSM: CT poverty	$IR_{st}$ (age standardized rate per 100,000)	Confidence Limits				Deaths	Person-time at risk
		Normal approximation		“Gamma” interval
		Lower	Upper	Lower	Upper
0.0-4.9%	0	(0.0	,0.0)	(0.0	,9.2)	0	40182
5.0-9.9%	3.5	-(0.5	,7.5)	(0.7	,10.3)	3	67458
10.0-19.9%	3.8	(0.1	,7.5)	(1.0	,9.7)	4	87336
20.0-100.0%	4.2	(1.4	,7.0)	(1.9	,8.0)	11	228288

4. Age-standardized incidence rate difference and rate ratio

Two commonly used measures for comparing incidence rates from two different groups are the incidence rate difference (IRD) and the incidence rate ratio (IRR). The incidence rate difference compares the rates on the absolute scale, and summarizes the excess rate comparing the larger to the smaller rate. The incidence rate ratio compares the rates on a relative scale, summarizing the size of one rate relative to the other rate.

To compare two age-standardized incidence rates on the absolute scale, the age-standardized incidence rate difference ( $IRD_{st}$ ) is the rate in one group minus the rate in the other, i.e. $IR_{st1} - IR_{st0}$ . The variance of this age-standardized incidence rate difference is simply the sum of the estimated variance of the two age-standardized rates $(4)$ ,

$\displaystyle Var \left({IRD} \right) = Var \left(IR_{st1} \right) + Var \left(IR_{st0} \right)$

To compare age-standardized rates from two different groups or regions on the relative scale, the age-standardized incidence rate ratio ( $\mbox{IRR}_{st}$ ) is simply $\mbox{IR}_{st1}$ / $IR_{st0}$ . Confidence intervals can be calculated using the variance estimator $(4)$ :

$\displaystyle Var \left[log \left(IRR_{st} \right) \right] = \frac {Var \left (IR_{st1} \right)}{{IR_{st1}}^2} + \frac {Var \left(IR_{st0} \right)}{{IR_{st0}}^2}$

Example:
To compare the age-standardized incidence rates in the most and least impoverished census tracts in Suffolk County, we start with the age-specific data for these two strata (note: for ease of presentation, we present variances in scientific notation in the table below):

ABSM: CT Poverty	Age category	Numerator	Denominator	$\mbox{w}_j$ (weight)	$\mbox{ IR}_j$ (age specific rate)	Var( $\mbox{IR}_j$ ) (variance of the age specific rate)	$\mbox{IR}_{st}$ (age standardized rate)	Var( $\mbox{IR}_{st}$ ) (variance of the age standardized rate)
0.0-4.9%	0-14	1	10,608	0.2147	0.000094	8.89E-09	0.007297	6.76E-08
0.0-4.9%	15-24	5	9,984	0.1386	0.000501	5.02E-08
0.0-4.9%	25-44	54	29,190	0.2982	0.00185	6.34E-08
0.0-4.9%	45-64	106	16,710	0.2221	0.006344	3.80E-07
0.0-4.9%	65+	657	15,825	0.1264	0.041517	2.62E-06
20.0-100.0%	0-14	182	155,193	0.2147	0.001173	7.56E-09	0.010193	1.77E-08
20.0-100.0%	15-24	170	217,593	0.1386	0.000781	3.59E-09
20.0-100.0%	25-44	831	288,882	0.2982	0.002877	9.96E-09
20.0-100.0%	45-64	1,291	108,588	0.2221	0.011889	1.10E-07
20.0-100.0%	65+	3,645	72,720	0.1264	0.050124	6.89E-07

The age-standardized rate difference is simply 1,019.3 per 100,000 – 729.7 per 100,000 = 289.6 per 100,000 (or, in scientific notation, 2.896 x 10-3).

Using the formula above, we calculate the variance of $\mbox{IRD}_{st}$ .

$\displaystyle Var \left({IRD}_{st} \right) = 6.76 \times 10^{-8} + 1.77 \times 10^{-8} = 8.54 \times 10^{-8}$

Then the lower and upper confidence limits are derived as follows:

$\displaystyle L_{IRDst} = 2.896 \times 10^{-3} - \left(1.96 * \sqrt{8.54 \times 10^{-8}} \right) = 0.002323$

$\displaystyle U_{IRDst} = 2.896 \times 10^{-3} - \left(1.96 * \sqrt{8.54 \times 10^{-8}} \right) = 0.003469$

or, expressed per 100,000, 232.2 to 346.9 per 100,000.

The age-standardized rate ratio is simply 1,019.3 per 100,000/729.7 per 100,000 = 1.40.

Using the formula above, we calculate the variance of log $\left(IRR_{st}\right)$ :

$\displaystyle Var \left[\mbox{log} \left(IRR_{st}\right) \right] = \frac {6.76 \times 10^{-8}}{0.007297^2} + \frac{1.77 \times 10^{-8}}{0.010193^2} = 0.001441$

Then the lower and upper confidence limits are derived as follows:

$\displaystyle L_{IRR_{st}} = \mbox{exp} \left[ \mbox{log} \left(1.40 \right) - 1.96\sqrt{0.001441 }\right] = 1.30$

$\displaystyle U_{IRR_{st}} = \mbox{exp} \left[ \mbox{log} \left(1.40 \right) - 1.96\sqrt{0.001441 }\right] = 1.50$

5. Relative Index of Inequality (RII)

Comparisons of socioeconomic gradients based on categorical ABSM may be complicated by differences in the population distributions of area-based socioeconomic measures. For example, it may be expected that the classifications producing smaller groups at the margins would lead to larger incidence rate ratios, comparing the most deprived to the most affluent, because finer discrimination of extremes of socioeconomic position is achieved. The relative index of inequality (RII) has been proposed as a measure which explicitly addresses this problem $(5-7)$ . Assuming ordinality of the ABSM categories, the RII is calculated by regressing the incidence rate in each ABSM category on the total proportion of the population that is more deprived in the socioeconomic hierarchy. Because the RII combines information about the magnitude of the socioeconomic gradient with information about the distribution of the socioeconomic variable in the population, it can be conceptualized as a measure of “total population input”.

In practice, this latter quantity is represented by the cumulative distribution function (cdf). We approximate the cdf for the jth level of a given ABSM by summing the proportion of the population represented by the categories $\mbox{ABSM}_1$ ,…, $\mbox{ABSM}_{j-1}$ , and adding one-half the proportion of the population represented by the category $\mbox{ABSM}_j$ .

Example:
In order to calculate the RII for poverty and all cause mortality in Massachusetts, we begin by calculating the approximate cumulative distribution function as follows:

ABSM: CT poverty	Population denominator	Proportion	Formula	Approximate cdf
0.0-4.9%	7,626,117	0.423	0.2115	0.211
5.0-9.9%	5,508,912	0.305	0.5755	0.576
10.0-19.9%	2,782,194	0.154	0.805	0.805
20.0-100.0%	2,120,208	0.118	0.941	0.941

In order to compare RII meaningfully across groups with differing age composition, we developed an age-standardized RII, standardized to the year 2000 standard million, as follows. Let observed $ij$ be the observed number of cases in the ith age group and the jth category of ABSM, and pop $ij$ be the population at risk in the corresponding category. First, we calculate the age-standardized rate IR $st$ in each stratum j defined by ABSM, as described above. For each stratum j, we estimate the expected number of cases in stratum j, $\mbox{expected}_{j}$ , by multiplying the age-standardized rate IR $st$ by the population denominator, pop $j$ = Σ $i$ pop $ij$ . We determine the “marginal” cumulative distribution function, cdf(ABSM $j$ ), of the ABSM over the entire population, as noted above.

Example:
The column of red numbers shows the expected number of cases in each poverty stratum.

ABSM: CT Poverty	IRst (age standardized rate per 100,000)	Observed deaths	Population denominator	Expected deaths	Approximate cdf
0-4.9%	757	57,256	7,626,117	57,731.70	0.211
5-9.9%	840.3	52,583	5,508,912	46,291.70	0.576
10-19.9%	915.9	27,730	2,782,194	25,482.00	0.805
20-100%	1,035.30	17,842	2,120,208	21,950.70	0.941

To calculate the age-standardized RIIst, we fit the following Poisson model for the expected cases:

$\displaystyle expected_{ij} \sim Poisson \left(\lambda_{ij} \right)$

$\displaystyle log \left(\lambda_{ij} \right) = log\left(pop_{ij}\right) + \beta_0 + \beta_1 * cdf\left(ABSM_j\right)$

Exponentiation of the $\beta_1$ yields the RII, which is interpretable as an incidence rate ratio comparing the rates in the bottom to the top of the socioeconomic hierarchy. A larger RII indicates a greater the degree of inequality across a socioeconomic hierarchy, which may be due to a steep socioeconomic gradient or large inequalities in the distribution of the ABSM itself.

Example:
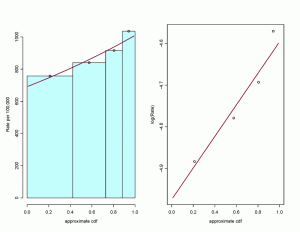
Fitting this model to the data presented above yields a $\beta_1$ of 0.379. Exponentiating this, we obtain an RII of 1.46. In the figures below, we can see how the RII for poverty is obtained. In the left figure, the height of light blue bars represents the all cause mortality rate per 100,000 in each of the four poverty strata (0-4.9, 5-9.9, 10-19.9, 20-100%), with width of bars proportional to population size of poverty stratum (in order from least to most impoverished). Open circles are plotted along the x-axis at the interpolated midpoints of each bar, approximating the cumulative distribution function of CT level poverty. The solid line represents fitted RII line. In the left figure, this line is not a straight line since the fitted line comes from a Poisson model. The right figure shows the plotted points and fitted RII line on the log scale, where the line is truly straight.

riiex_revised

6. Population Attributable Fraction

The population attributable fraction (PAF) is a useful summary measure for characterizing the public health impact of an exposure on population patterns of health and disease. It is defined as “the fraction of all cases (exposed and unexposed) that would not have occurred if exposure had not occurred.” $(8)$ For a polytymous exposure, the population attributable fraction is a weighted sum of the attributable fractions for each level of the exposure, with the weights defined by the case fractions (number of exposed cases divided by overall number of cases):

$\displaystyle PAF = CF_1 \times \frac{RR_1 - 1}{RR_1} + CF_2 \times \frac{RR_2 -1}{RR_2} + ... + CF_j \times \frac{RR_j - 1}{RR_j}$

In order to aggregate multiple PAFs over several age strata i=1,…,I, note that

$\displaystyle PAF_{agg} = \frac{\sum_i \mbox{excess number of cases}}{\mbox{number of cases}}$

$\displaystyle = \frac {\sum_i \mbox{number of cases} \times \frac {\mbox{excess number of cases}}{\mbox{number of cases}}}{\sum_i\mbox{number of cases}}$

$\displaystyle =\frac {\sum_i \mbox{number of cases} \times PAF_1}{\sum_i\mbox{number of cases}}$

that is, a weighted average of stratum specific PAFs, with the number of cases in each age stratum as weights.

Example:
To calculate the population attributable fraction of all cause mortality due to poverty, we begin by tabulating the cases and population person-time at risk in each poverty stratum j within each age group i. Within each age group, the case fraction $\mbox{CF}_{ij}$ is the number of cases in that poverty stratum, divided by the total number of cases within the age group. The incidence rate ratio $\mbox{IRR}_j$ for a particular poverty stratum, relative to the reference category of the least impoverished group, is calculated by dividing the rate in that poverty stratum by the rate in the least impoverished group. For each age stratum, we calculate a separate age-specific PAF, as seen in the column of red numbers in the table below. These age-specific PAFs range from 5% to 23%.

Age category (i)	ABSM: CT poverty (j)	Cases	Person-time denominator	Rate per 100,000	Case Fraction ( $\mbox{CF}_{ij}$ )	Incidence rate ratio ( $\mbox{IRR}_{ij}$ )	Population attributable fraction ( $\mbox{PAF}_i$ )
0-14	0-4.9% (reference)	303	727,947	41.6	40.7%	1.00	0.1626
	5.0-9.9%	253	461,958	54.8	34.0%	1.32
	10.0-19.9%	113	206,214	54.8	15.2%	1.32
	20.0-100.0%	75	100,716	74.5	10.1%	1.79
	Total cases:	744

15-24	0-4.9% (reference)	377	510,645	73.8	40.6%	1.00	0.0506
	5.0-9.9%	323	349,518	92.4	34.8%	1.25
	10.0-19.9%	152	179,928	84.5	16.4%	1.14
	20.0-100.0%	76	153,273	49.6	8.2%	0.67
	Total cases:	928

25-44	0-4.9% (reference)	1,569	1,201,002	130.6	34.7%	1.00	0.2266
	5.0-9.9%	1,392	873,072	159.4	30.7%	1.22
	10.0-19.9%	933	405,366	230.2	20.6%	1.76
	20.0-100.0%	633	200,457	315.8	14.0%	2.42
	Total cases:	4,527

45-64	0-4.9% (reference)	5,314	763,464	696.0	39.7%	1.00	0.2210
	5.0-9.9%	4,429	461,451	959.8	33.1%	1.38
	10.0-19.9%	2,287	191,934	1,191.6	17.1%	1.71
	20.0-100.0%	1,369	82,674	1,655.9	10.2%	2.38
	Total cases:	13,399

65+	0-4.9% (reference)	19,470	376,002	5,178.2	38.8%	1.00	0.0725
	5.0-9.9%	17,784	314,181	5,660.4	35.4%	1.09
	10.0-19.9%	8,734	146,091	5,978.5	17.4%	1.15
	20.0-100.0%	4,248	63,594	6,679.9	8.5%	1.29
	Total cases:	50,236

To aggregate these PAFs across age strata, we weight the contribution of each age stratum by the proportion of cases in that age stratum. As seen in the table below, this results in an aggregated population attributable fraction $\mbox {PAF}_{agg}$ of 11%.

Age category (i)	Cases	Population attributable fraction ( $\mbox{PAF}_i$ )	$\rightarrow$	Aggregated population attributable fraction ( $\mbox{PAF}_{agg}$ )
0-14	744	0.1626	(7440.1626 + 9280.0506 + 45270.2266 + 133990.2210 + 50236*0.0725)/ 69834	=0.1116
15-24	928	0.0506
25-44	4,527	0.2266
45-64	13,399	0.221
65+	50,236	0.0725
Total cases:	69,834

REFERENCES

1. Breslow NE, Day NE (eds). Statistical Methods in Cancer Research, Vol. II: The Design and Analysis of Cohort Studies. Oxford, UK: Oxford University Press, 1987.

2. Anderson RN, Rosenberg HM. Age standardization of death rates: implementation of the year 2000 standard; National Vital Statistics Reports: Vol 37, No. 3. Hyattsville, MD: National Center for Health Statistics, 1998.

3. Fay MP, Feuer EJ. Confidence intervals for directly standardized rates: a method based on the gamma distribution. Statistics in Medicine 1997;16:791-801.

4. Rothman KJ, Greenland S. Modern Epidemiology. 2nd Edition. Philadelphia: Lippincott-Raven, 1998.

5. Pamuk ER. Social class inequality in mortality from 1921 to 1972 in England and Wales. Popul Stud 1985;39:17-31.

6. Wagstaff A, Paci P, van Doorslaer E. On the measurement of inequalities in health. Soc Sci Med 1991;33:545-57.

7. Davey Smith G, Hart C, Hole D, et al. Education and occupational social class: which is the more important indicator of mortality risk? J Epidemiol Community Health 1998;52:153-60.

8. JA Hanley, A heuristic approach to the formulas for population attributable fraction. J Epidemiol Community Health 2001;55:508-514.